Switching on Pecan - HO Scale Modern Minimalist Switching Layout

TWO TRACKS, ONE SWITCH - WHERE'S THE FUN IN THAT?

The trackplan of a "tuning fork" layout tends to be deceiving.

The bare bones simplicity of having nothing but an approach spur, a switch, and two tracks beyond that, seems to suggest very limited (if any) operational interest. But that's because we tend to look at such a simple trackplan the wrong way.

The operational "spice" of switching a "tuning fork" layout is not generated by the trackplan, but rather by the way the spurs are switched - by using so-called car spots.

Car spotting takes place where one track (such as a single spur running alongside a warehouse) either serves multiple customers in that structure or has different areas for loading and unloading.

Different US railroads use(d) differing terminology for this car spot designation system; the acronym SPINS is an abbreviation for Southern Pacific Industry Numbering System - it originated on the SP but was also used by e.g. BN. CLIC (Car Location Identity Codes) was a Santa Fe term for the same thing, as was ZTS (Zone, Track, Spot) on Conrail.

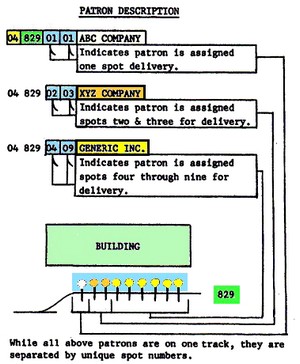
The example shown here (taken from a 1987 Conrail ZTS for its New England Division) explains it all quite well. If a freight car is to be set out at 04-829-07, then the ZTS map will tell any crew that its destination is car spot 07 on track 829 in Zone 04, and that the customer in question is the Generic Inc.

It is easy to see how requiring freight cars to be placed in specific spots can add not only additional realism to a switching layout but also beef up the challenge of operating it considerably.

And just like that, a single industrial spur isn't that simple to switch anymore.

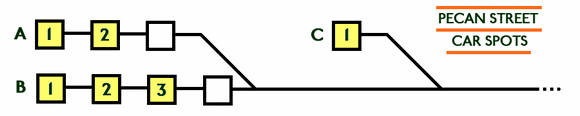
Pecan Street has five such car spots, two directly in front of the warehouse and three on the adjacent spur. The standard "tuning fork" formula is expanded by the single spot at the cold storage (C).

Applying the core idea of the Conrail ZTS system, Pecan Street provides the option to switch these car spots with as many (or as few) cars and according to whatever scheme comes to mind and hits your operational fancy - you could use switching orders, draw card orders, or even just make up switching moves as you go along.

In the real world and under normal circumstances, the two tracks serving the warehouse would hardly ever see a big congregation of boxcars, and this too can easily be replicated.

Using car spots to determine where rolling stock is picked up or dropped off, the complexity of switching a "tuning fork" will vary according to the number of cars in use. Possibly just for the fun of running a favourite locomotive and a few colourful boxcars, this can provide a relaxing fifteen or so minutes of easy-going operation.

SWITCHING PUZZLE MODE

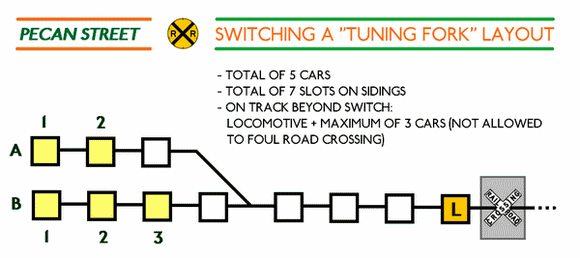
In order to operate a tuning fork layout such as Pecan Street as a switching puzzle, certain constraints must be introduced as to how many items of rolling stock can go where.

The number of car spots on Pecan Street reflects the capacity limits of the two sidings; two directly in front of the warehouse and three on the adjacent spur, with a "free spot" on both sidings.

In addition, switching puzzles also call for a capacity restriction to the spur leading up to the switch for those two tracks, i.e. the headshunt track - an artifical complication of the situation. In real life, the train crew might well be able to pull out all the boxcars that would possibly fit on both sidings in one move; by not allowing this, the puzzle aspect is introduced.

After a few trial runs on paper, I found that restricting the capacity of the approach track to a maximum of 3 boxcars plus the locomotive provided the necessary wiggleroom to produce solvable puzzle set-ups; a lower capacity (2 cars plus loco) can result in situations where a boxcar gets stuck at the end of the longer spur because it cannot be pulled.

All of this results in the "tuning fork switching puzzle" formula "2(+1) / 3(+1) / 3+L".

The capacity boundary of the approaching track on Pecan Street is marked by a road crossing, implying some sort of a rule in place here that the crossing may not be blocked for switching moves.

The actual lengths of track needed for this switching puzzle are, of course, directly related to the rolling stock used. Since I wanted 50' boxcars and second generation four-axle road-switchers (e.g. an EMD GP38), this resulted in the extended length of Pecan Street; using 40' boxcars and a short locomotive (e.g. a GE 44t switcher) will reduce the overall length of the layout considerably.

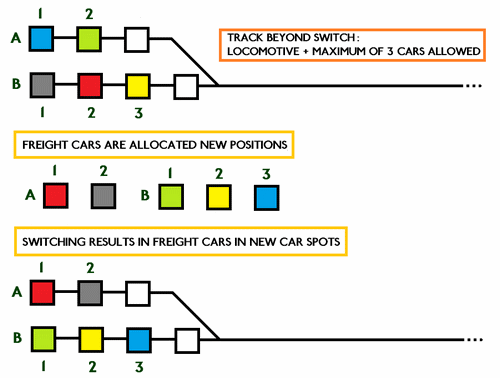At the start of the swicthing puzzle, five items of rolling stock occupy all of the five car spots.

Each item of rolling stock is then allocated a new car spot (in some cases, this will coincidentally be the same spot it is sitting in at the outset).

The goal of the puzzle (and thus the task of the operator) is to switch the rolling stock to the newly designated spots.

The car spots will most likely be decided by an element of chance (e.g. by drawing car cards or rolling a dice), but the rolling stock could also be switched around according to requirements set by the operator.

Things can be made more challenging by introducing either an element of trying to keep the number of moves to a minimum or by setting a time limit.

Most of the time, this will prove to be a not too challenging switching puzzle, although certain set-ups can require some advance planning of the "pull out, shove in" switching moves. In that respect, it is not unlike an Inglenook Sidings layout, albeit with a significantly reduced complexity.

Overall view of the warehouse tracks with a typical set-up on Pecan Street in switching puzzle mode

And although it is unlikely that a tuning fork switching puzzle will keep you entertained for hours on end, it does provide the opportunity of having short but pleasant interludes of operation on a layout that does not take up a lot of space, is easy to set up and store away, and can be built in a reasonable amount of time and on a modest (or even minimal) budget.

more to come on possible ways to select car spots and how to run the puzzle

page created 12 March 2022
last updated 21 January 2023